| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 사후 가지치기
- C4.5
- 체인지업후기
- 아다부스트
- pre pruning
- 의사결정나무
- MultipleLinearRegression
- cost complexity pruning
- 회귀분석
- 경사하강법
- boosting
- 군집화기법
- 정보이득
- Adaboost
- AdaBoostRegressor
- 중선형회귀
- LeastSquare
- 최소제곱법
- 선형모형
- 실제데이터활용
- 선형회귀
- AdaBoostClassifier
- 부스팅기법
- 부스팅
- 사전 가지치기
- LinearRegression
- 캘리포니아주택가격예측
- KNearestNeighbors
- gradientdescent
- post pruning
- Today
- Total
데이터 분석을 향한 발자취 남기기
3. 로지스틱 회귀분석 (Logistic Regression) 본문
우리가 예측하고자 하는 값이 실수, 연속적인 값을 갖는 경우 선형회귀분석을 이용해 이를 설명하는 모델을 탐색한다. 하지만, 만약 우리가 예측하고자 하는 값이 "예/아니오", "10대/20대/30대"와 같이 분류 문제가 주어지면 어떻게 해야할까? 로지스틱 회귀분석은 이러한 분류 문제를 해결하기 위한 방법이다. 로지스틱 회귀분석을 사용하면 수학쪽지시험을 통과할 수 있을까? 에 대해 "90%의 확률로 통과한다"와 같이 답변할 수 있다.
오늘은 로지스틱 회귀분석을 이해하고 유도해보고자 한다.
0. 시그모이드 함수
1. 로지스틱 회귀분석
2. 최대우도법
3. 경사하강법
0. 시그모이드 함수
$(-\infty, \infty)$ 사이 값을 예측하는 선형회귀분석과 달리 로지스틱 회귀분석은 $[0, 1]$ 사이 확률 값을 출력한다. 이때, 예측값이 $[0, 1]$ 사이 값을 가질 수 있도록 시그모이드 함수를 사용한다. 시그모이드 함수란 유한한 구간 내 한정된 값을 가지고 항상 양의 기울기로 단조 증가하는 함수를 의미한다.
시그모이드 함수의 종류는 다양하지만, 일반적으로 로지스틱 회귀분석에서 시그모이드 함수로 로지스틱(logistic) 함수를 사용한다.

범위 제한 방법
#1. $[0, 1]$ → $(-\infty, \infty)$
$p$는 1이 나올 확률이라 했을 때, 확률 값이므로 $[0, 1]$ 사이 값을 갖는다. 이때, 이 $p$는 아래 식을 이용해 $[0, \infty)$ 사이 값을 갖도록 변환할 수 있으며 이를 승산비($odds$)라 한다.

이때, 변환된 $p$는 로그함수를 통해 변환한다.


x값은 양수의 값만 가지지만, 로그변환을 통해 $(-\infty, \infty)$의 값을 가질 수 있다.
#2. $(-\infty, \infty)$ → $[0, 1]$
반대로 $(-\infty, \infty)$ 사이 값을 $[0, 1]$로 제한하는 방법을 알아보자. 이는 #1에서 구한 $logit(odds)$의 역함수를 계산하면 된다. 이번에는 $p$가 $(-\infty, \infty)$ 사이 값을 갖는다고 가정하자.

* 역함수 유도 과정

위에서 구한 식은 로지스틱 함수의 형태와 동일하다. 즉, 로지스틱 함수를 이용해 범위를 제한할 수 있음을 알 수 있다.
+ 로지스틱 함수 (Logistic function)
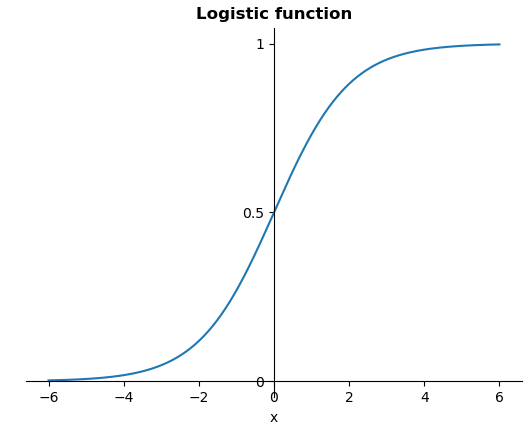

1. 로지스틱 회귀분석
로지스틱 회귀분석은 항상 0 ~ 1 사이 값을 갖기 때문에, "0 또는 1을 분류할 때, 출력값이 0.9이면 90%의 확률로 1이다"와 같이 해석할 수 있다. 로지스틱 회귀분석의 가설함수 형태는 다음과 같이 주어진다.

그렇다면 위 식은 선형함수일까?
정답은 비선형함수이다.
모든 $j = 1, \cdots , k$에 대해, 우리가 추정해야하는 회귀계수인 $w_{j}$에 대해서 가설함수를 편미분하면 $w_{j}$를 제외한 나머지 회귀계수가 없는 경우 이를 선형함수라 한다. 하지만 아래 예시에서 볼 수 있듯, $w_{0}$에 대해 편미분했지만 여전히 $w_{1}$이 있음을 볼 수 있다.

- 비용함수
일반적으로 선형회귀분석에서 경사하강법을 적용할 때, 비용함수는 다음과 같다.

이를 로지스틱 회귀분석에 그대로 적용하게 되면 선형회귀분석에서는 convex했던 비용함수가 non-convex한 함수 형태로 변화한다.
즉, 하나의 최솟값이 아닌 다수의 local minimum이 발생해 비용함수를 최소화하기 어렵다.
 |
|
| 선형회귀분석 |
로지스틱 회귀분석 |
 |
 |
* 로지스틱 회귀분석의 비용함수를 최소화하기 어려운 이유
: 시작점을 어디에 잡느냐에 따라 경사하강법에 의해 찾아지는 최솟값이 다를 수 있음
따라서, 로지스틱 회귀분석에서는 비용함수를 새롭게 정의해 convex한 형태로 만든다. $h(w)$는 로지스틱 함수를 통한 가설함수, $y$는 실제값이라 가정했을 때, 정의되는 비용함수는 다음과 같다.

 |
 |
만약, y가 1이면 가설함수의 값이 1에 가까울수록 적은 비용을 갖고, y가 0이면 가설함수의 값이 0에 가까워질수록 적은 비용을 갖도록 설정되었다. 이는 최대우도추정법에 의해 추정되며, 이를 하나의 함수로 나타내면 다음과 같다.

2. 최대우도추정
간단하게 최대우도추정으로 어떻게 비용함수의 형태가 유도되었는지를 살펴보고자 한다.
최대우도추정을 하기 위해서, 실제값의 분포의 확률분포를 가정한다.
로지스틱 회귀분석에서는 종속변수 $y$가 베르누이 확률분포를 따른다고 가정하자.
- 베르누이 분포 --------------------------------------------------------------------------------------------------
확률변수 $X$가 항상 0 또는 1의 값을 갖는다면 $X$의 확률분포는 베르누이 분포인 $B(1, p)$를 따른다고 한다. 이때, $p$는 $X$가 1일 확률이다.
$P(X = x) = p^{x}(1-p)^{1-x}, x = 0, 1$
---------------------------------------------------------------------------------------------------------------------
가설함수 $h_{w}(x)$가 1일 확률일 때, y의 분포 $p(y|x)$는 다음과 같다.

$p(y|x) = h(x)^{y} (1-h(x))^{1-y}$
데이터 ${x_{i}, y_{i}}, i = 1, \cdots , N$에 대해 전체 데이터에 대한 로그우도함수($LL$)는 다음과 같이 정의된다. (우도함수의 최댓값을 탐색할 때, 계산을 좀더 쉽게 하기 위해 우도함수에 로그를 씌워 계산함)
$LL = log(\prod^{n}_{i=1} h(x_{i})^{y_{i}}(1-h(x_{i}))^{1-y_{i}})$
= $\sum_{i=1}^{n}(y_{i} log (h(x_{i})) + (1-y_{i}) log (1-h(x_{i}))$ *
* 이 식이 로지스틱 회귀분석의 비용함수로 사용된다.
로지스틱 회귀분석에서 파라미터를 추정하기 위해, 최대우도를 최대화하는 모수를 추정해야하지만, 미분된 로그우도함수가 비선형 함수라 구할 수 없다. 따라서, 이를 수치적으로 최대화하는 방법인 경사하강법을 이용한다.
3. 경사하강법
경사하강법은 기울기를 이용해 파라미터를 업데이트하기 때문에 비용함수에 대해 미분한 함수를 계산해야한다. 비용함수를 최소화하는 파라미터를 찾는 것이 목적이므로 로그우도를 최대화하는 모수를 찾기 위해 $J = -\frac{LL}{N}$을 최소화한다. 즉 로지스틱 회귀모형의 비용함수는 다음과 같다.
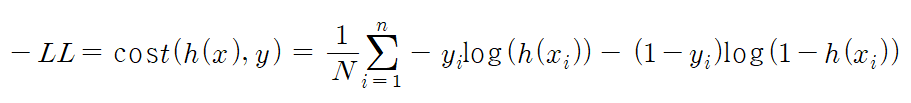
- 로그우도함수 미분
복잡한 형태의 식에 대한 미분을 쉽게 하기 위해 chain rule을 이용하면, 다음과 같이 미분 결과를 생성한다.


마지막으로 학습률 $\alpha$를 곱해줌으로써 파라미터는 다음과 같이 업데이트 한다.

오늘은 분류에서 흔히 쓰이는 로지스틱 회귀분석에 대해서 정리했다. 이진 클래스 분류를 중점으로 다뤘지만, 로지스틱 회귀분석은 다중 클래스 분류에도 쓰일 수 있다.
다음 포스트에서는 다중 클래스 분류에서 로지스틱이 어떻게 사용되는지 보고 설명변수가 많은 데이터에 대해 경사하강법을 이용하여 선형회귀 및 로지스틱 회귀분석을 진행해보고자 한다.
참고 자료
- "6.1 로지스틱 회귀분석", 데이터 사이언스 스쿨, 2023년 2월 28일 접속,
- "앤드류 응의 머신러닝(6-5): 로지스틱회귀 경사 하강법", 브런치, 2023년 2월 28일 접속,
'손으로 직접 해보는 모델정리 > 단일 모델' 카테고리의 다른 글
| 5. 경사하강법을 이용한 로지스틱 회귀 (0) | 2023.03.18 |
|---|---|
| 4. 경사하강법을 이용한 선형회귀 (0) | 2023.03.08 |
| 2. 경사하강법 (Gradient Descent) (0) | 2023.01.04 |
| 1. (다)중선형회귀분석 (Multiple Linear Regression Analysis) (0) | 2022.12.26 |
| 0. 단순선형회귀분석 (Simple Linear Regression Analysis) (0) | 2022.12.19 |





