| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- AdaBoostClassifier
- 선형회귀
- 중선형회귀
- 부스팅기법
- post pruning
- KNearestNeighbors
- LinearRegression
- 의사결정나무
- 부스팅
- gradientdescent
- pre pruning
- AdaBoostRegressor
- 체인지업후기
- 캘리포니아주택가격예측
- boosting
- MultipleLinearRegression
- 군집화기법
- 사전 가지치기
- 회귀분석
- 아다부스트
- LeastSquare
- 경사하강법
- 최소제곱법
- 정보이득
- Adaboost
- 실제데이터활용
- C4.5
- cost complexity pruning
- 선형모형
- 사후 가지치기
- Today
- Total
데이터 분석을 향한 발자취 남기기
7. 의사결정 나무(Decision Tree) 본문
오늘은 대표적인 트리 모형인 Decision Tree에 대해서 공부하고자 한다. 먼저 Decision Tree에 대한 구조를 살펴보고, Decision Tree를 구성하는데 사용되는 알고리즘인 ID3, C4.5, CART에 대해서 알아보고자 한다.
0. Decision Tree란?
1. ID3
2. C4.5
3. CART
0. Decision Tree란?
의사결정 나무(Decision Tree)는 데이터에 있는 규칙을 학습을 통해 자동으로 찾아내 트리 기반 분류 규칙을 생성하는 모델이다. 생성된 모델의 모양이 나무와 같다고 하여 결정 트리라 불린다.

- 규칙 노드: 규칙 조건(분류 기준)
- 리프 노드: 분류 및 예측값
새로운 데이터가 들어오면 루트 노드를 기준으로 규칙 노드를 거치면서 최종적으로 위치한 리프 노드의 예측값으로 예측하게 된다. 이때, 분류 문제이면 루트 노드 내 샘플들 중 가장 빈도가 높은 클래스로 예측하고, 회귀 문제이면 샘플들의 종속변수 평균값으로 예측한다.
특징
의사결정 나는 머신러닝 알고리즘 중 직관적으로 이해하기 쉬운 모델이며 학습 결과를 시각화하여 보일 수 있다는 장점이 존재한다. 또한, 서포트 벡터 머신(SVM)이나 KNN은 데이터 전처리가 모델 성능에 크게 영향을 미치지만, 결정 트리는 각 피처를 별도로 처리하기 때문에 이에 대한 영향을 덜 받는다. 하지만! 복잡한 규칙 구조를 갖고 있기 때문에 과적합이 발생하기 쉬우며 이로 인해 예측 성능이 저하될 수 있다.
| 장점 | 단점 |
| - 쉽고 직관적임 - 피처의 스케일링 및 정규화 등 사전 가공 영향도가 크지 않음 |
- 과적합으로 인해 알고리즘의 성능이 떨어짐 |
적은 결정 노드로 높은 예측도를 달성하려면 균일한 데이터 세트를 구성하도록 분할하는 것이 중요하며, 이를 불순도를 줄여나가는 방법으로 분할한다고 표현한다.
* 불순도

불순도는 데이터 집합 내 다른 클래스의 샘플이 얼마나 혼합되어 있는지를 나타내는 척도를 의미한다. 색에 따라 클래스가 다르게 부여되었다고 가정했을 때, A보다 B에 여러 클래스의 샘플들이 혼합되어있음을 볼 수 있다. 즉, A보다 B의 불순도가 더 크다.
의사결정 나무를 생성하는 알고리즘은 대표적으로 ID3, C4.5, CART가 있으며, 각 알고리즘에 따라 여러 특징을 갖고 있다. 따라서, 각 알고리즘에 대해서 알아보고 어떤 식으로 의사결정 나무를 생성하는지 예제를 통해 알아보고자 한다.

1. ID3 (Iterative Dichotomiser 3)
ID3는 범주형 변수에만 적용할 수 있는 결정트리 알고리즘으로 정보 이득(Information Gain)을 기준으로 분할을 수행한다. 정보 이득은 데이터를 분할하기 전과 후의 불순도 차이로 계산된다. 이때, 불순도는 엔트로피(Entropy)를 이용해 계산한다.
- 엔트로피 (Entropy)

ID3는 엔트로피를 이용해 노드 내 불순도를 측정한다. 이때, $C$는 클래스, $p_{i}$는 클래스 $i$를 뽑을 확률을 나타낸다.
* 정보 이득 (Information Gain)

- 분기 전 엔트로피 $H(S)$
- 분기 후 $t_{1}$에 해당하는 그룹의 엔트로피 $H(S, t_{1})$
- 분기 후 $t_{2}$에 해당하는 그룹의 엔트로피 $H(S, t_{2})$
정보 이득은 분기 전후 엔트로피 차이값으로 계산된다. 이때, 분기 후 엔트로피는 양쪽 가지로 나뉠 확률을 곱해 계산한다.
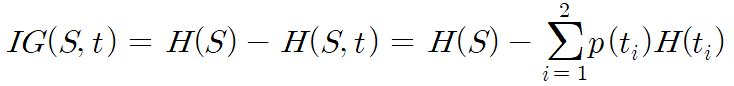
정보이득을 통해 엔트로피가 얼마나 감소했는지를 측정한다. 따라서, 정보 이득이 높을수록 불순도가 크게 줄어들었음을 의미하므로 정보 이득이 최대화하는 분류 기준을 선택하게 된다.
- 예제

우리는 Outlook, Temperature, Humidity, Windy를 이용해 Play를 예측하는 트리를 생성하고자 한다.
1) 분기 전 엔트로피 계산
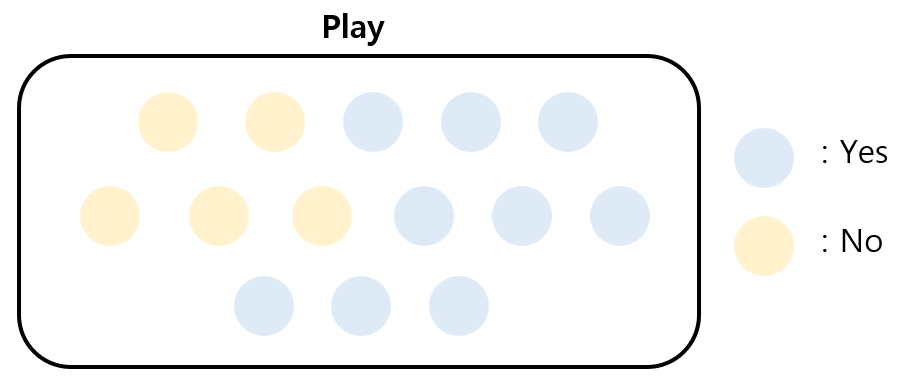

$p_{Yes}$는 Play 변수 중 Yes일 확률로 계산되며, 이를 이용해 Yes에 대한 엔트로피를 계산한다. 이를 No에 대해서도 계산하면 분기 전 엔트로피는 0.94임을 알 수 있다.
2) 분기 후 엔트로피 계산
설명변수 중 Outlook을 예제로 들어 설명하고자 한다. Outlook은 sunny, overcast, rain으로 3개의 class를 갖고 있는 변수이다. 먼저, 각 class마다 Play의 분포를 확인하고 각 class마다 엔트로피를 계산한다.

- sunny 엔트로피

- overcast 엔트로피

- rain 엔트로피

분기 후 엔트로피는 각 class마다 계산되기 때문에, 범주형 변수에만 적용할 수 있는 알고리즘임을 알 수 있다!
3) 정보 이득 계산


$p(sunny)$는 Play 중 Outlook이 sunny에 속할 확률로 계산되며 이를 sunny 엔트로피에 곱해주면 된다. 따라서, 정보 이득은 0.694임을 볼 수 있다.
이를 다른 설명변수에 대해서도 수행해 가장 높은 정보 이득을 갖는 설명변수로 Play를 분류한다. 더이상 분할할 수 없을 때까지 반복하면 의사결정 나무가 생성된다.
참고자료
https://tyami.github.io/machine%20learning/decision-tree-2-ID3/
의사결정 나무 (Decision Tree) ID3 알고리즘 설명
의사결정 나무의 기본 알고리즘 중 하나인 ID3 를 공부해봅시다
tyami.github.io
2. C4.5
ID3는 무조건 불순도가 낮은 경우만을 고려하기 때문에 모든 leaf node가 단 하나의 샘플을 갖더라도 불순도가 낮은 의사결정 나무로 판단한다. 즉, 이러한 이유로 일반화 성능이 매우 낮아진다(과적합할 위험이 큼). C4.5는 ID3의 확장된 버전으로 이를 정보 이득 비율 (Information Gain Ratio)을 사용하여 해결한다. 또한, 분류 문제에서만 사용할 수 있는 ID3와 달리 연속적인 피처와 결측치를 처리할 수 있다.
* 정보 이득 비율 (Information Gain Ratio)


$IG$는 ID3에서 구한 정보 이득을 의미하며, $IV$는 Instrinsic Value를 의미한다. $N$은 생성된 가지의 수, $p_{i}$는 이번엔 $i$번째 가지에 해당하는 확률이다.
- 예제


앞에서 구한 $IG(Play, Outlook) = 0.694$였다. 이를 $IV$로 나누어주면 결국 정보 이득 비율은 0.44임을 알 수 있다. 이처럼 정보 이득 비율을 사용함으로써 피처의 분할 능력에 대한 편향을 줄이고 범주형 뿐만 아니라 연속적인 피처를 다룰 수 있다. 또한, 결측치가 있는 데이터를 처리할 수 있는 기능을 갖추고 있다.
참고자료
https://tyami.github.io/machine%20learning/decision-tree-3-c4_5/
의사결정 나무 (Decision Tree) C4.5 알고리즘 설명
의사결정 나무의 기본 알고리즘 중 하나인 C4.5 를 공부해봅시다
tyami.github.io
3. CART (Classification and Regression Trees)
CART는 이름에서도 알 수 있듯이 범주형, 숫자형 변수에 모두 적용할 수 있는 결정 트리 알고리즘으로 분류에서는 지니 계수 (Gini Index)를 사용하고 회귀에서는 오차(ex. RSS, MSE)를 기준으로 트리를 생성한다. 분류 문제에서는 각 클래스의 비율을 고려해 최적의 분할을 수행하고 회귀 문제에서는 분할 전후의 예측 변수의 분산을 최소화하는 방향으로 분할을 수행한다.
* CART는 앞의 ID3, C4.5와 달리 여러 자식 노드를 갖지 않고 단 두개의 노드로 분기하는 Binary tree구조를 보인다.
* 지니 계수 (Gini Index)
지니 계수는 불순도를 측정하는 지표로 데이터의 통계적 분산정도를 정량화해 표현한 값이다. 지니 계수가 높을수록 데이터가 분산되어있음을 나타내며 따라서, CART는 지니 계수가 높은 쪽으로 트리를 생성한다.

이때, $p_{i}$는 클래스 $i$를 뽑을 확률을 나타낸다.
- 예제


Binary Tree의 구조를 갖고 있기 때문에, Outlook의 각 클래스마다 지니 계수를 계산해줘야한다.
1) sunny

"Outlook = sunny인지 아닌지"에 따라 Play를 분류하면 (A)와 (B)로 나눠질 수 있으며, 각 노드에 대해서 지니 계수를 계산한다.
(A)의 지니 계수

(B)의 지니 계수

최종적으로 Outlook = sunny에 대한 지니 계수는 (A), (B) 지니 계수에 각각 양쪽 가지로 나뉠 확률을 곱해주어 계산한다.

Outlook이 overcast 혹은 rain 인지 아닌지에 대해서 모두 계산을 하면 다음과 같다.
2) overcast

(A)의 지니 계수

(B)의 지니 계수


3) rain

(A)의 지니 계수

(B)의 지니 계수


Outlook이 rain인지 아닌지로 분류했을 때, 지니 계수가 가장 작으므로 가장 잘 분류하는 기준임을 알 수 있다. 이를 나머지 설명변수에도 모두 적용한 후, 가장 작은 지니 계수를 갖는 분할 조건으로 설정하면서 의사결정 나무를 생성한다.
참고자료
의사결정나무(Decision Tree) :: CART 알고리즘, 지니계수(Gini Index)란?
이전 포스팅에서 의사결정나무란 무엇인지, 어떤 기준으로 모델을 만들어가며 불순도가 무엇인지와 ID3 알고리즘에 대해 소개했다. 지난 포스팅 바로가기 https://leedakyeong.tistory.com/entry/Decision-Tree
leedakyeong.tistory.com
오늘은 의사결정 나무에 대해서 간단히 살펴보고, 이를 생성하는 여러 알고리즘에 대해서 알아보았다. 다음 포스트는 CART 알고리즘 기반으로 분류 및 회귀 트리를 생성해보고 가지치기에 대해서 공부하고자 한다.
'손으로 직접 해보는 모델정리 > 단일 모델' 카테고리의 다른 글
| 8. Decision Tree Pruning (의사결정 나무 가지치기) (0) | 2023.06.12 |
|---|---|
| 6. KNN: K Nearest Neighbors (0) | 2023.05.12 |
| 5. 경사하강법을 이용한 로지스틱 회귀 (0) | 2023.03.18 |
| 4. 경사하강법을 이용한 선형회귀 (0) | 2023.03.08 |
| 3. 로지스틱 회귀분석 (Logistic Regression) (0) | 2023.02.28 |




